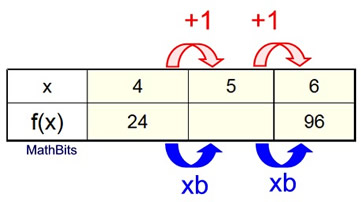
We DO KNOW that this is an exponential function since the question says it is an exponential function.

| 24 • b • b = 96 → 24b 2 = 96 → b 2 = 4 → b = 2 We now have: f (x) = a • 2 x To get a, substitute one of the points, such as (4,24). 24 = a • 2 4 = a • 16 → a = 24/16 = 1.5 |
"Do two points always determine an exponential function?"
Assuming that we are speaking about an exponential function of the form f (x) = ab x , the answer is "Yes, under certain conditions." The conditions are that (1) a ≠ 0 (because you would have a straight line), (2) that the x-coordinates not be the same (you wouldn't have a function) and (3) that the y-coordinates of the points be non-zero with the same signs (remember the asymptotic nature of the graphs of these exponential functions - always all above, or all below, the x-axis).
So, how do we change two points into an exponential function?
Constructing functions given only two input-output pairs (or ordered pairs) can be accomplished in a variety of ways. The choice of solution method will depend upon the nature of the given pairs. For example, if you are given the y-intercept as one pair, the solution will be fast and easy. If, on the other hand, you are given two generic pairs, perhaps containing decimals, you will need to do more work to find the solution. Let's take a look at some of the possibilities.
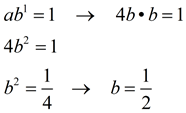
Plug a into second equation:
Solution:
Substitute the points into the formula:
(1, 30) → f (1) = ab 1 = 30
(3,187.5) → f (3) = ab 3 = 187.5
Plug in to find a :
Solution:
Substitute the points into the formula:
(-3, 256) → f (-3) = ab -3 = 256
(2,¼) → f (2) = ab 2 = ¼
Remember not to round until you reach the final answer. The slightest change in b can affect the answer. If not "asked" to round, leave the full calculator entry.
Plug in to find a :
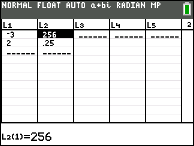
Solution:
Enter the two points into L1 and L2 under STAT
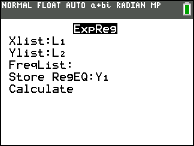
Be sure your lists match where you stored the points. Fill in Y1 if you want to see the graph.
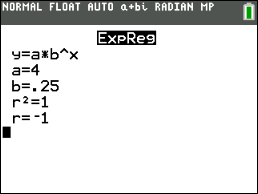
Aren't calculators wonderful!!
![]()
NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use".